Calculating Reacting Masses, Solutions & Concentrations of Solutions in g/dm3 & mol/dm3
Calculating percentage composition, moles, mass and relative formula mass
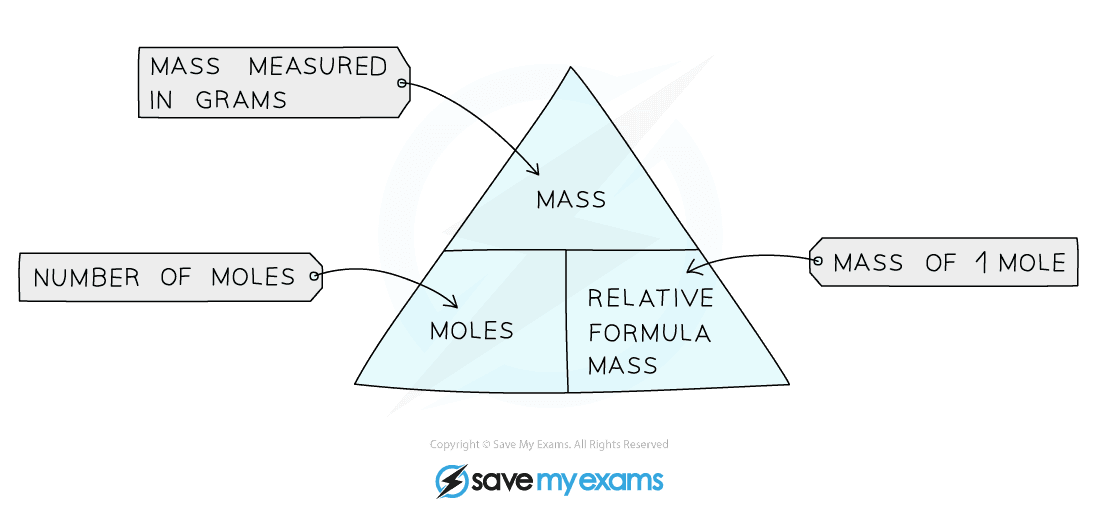
Formula triangle for moles, mass and formula mass
1. Calculating Moles
Equation:
Amount in Moles = Mass of Substance in grams ÷ Mr (or Ar)
Example:
2. Calculating Mass
Equation:
Mass of substance (grams) = Moles x Mr (or Ar)
Example:
3. Calculating Relative Formula Mass
Equation:
Mr (or Ar) = Mass of Substance in Grams ÷ Moles
Example:
10 moles of Carbon Dioxide has a Mass of 440 g. What is the Relative Formula Mass of Carbon Dioxide?
Relative Formula Mass = Mass ÷ Number of Moles
Relative Formula Mass = 440 ÷ 10 = 44
Relative Formula Mass of Carbon Dioxide = 44
4. Calculating Percentage Composition
- The percentage composition is found by calculating the percentage by mass of each particular element in a compound
Example:
Calculate the percentage of oxygen in CO2
Step 1 – Calculate the molar mass of the compound
Molar mass CO2 = (2 x 16) + 12 = 44
Step 2 – Add the atomic masses of the element required as in the question (oxygen)
16 + 16 = 32
Step 3 – Calculate the percentage
% of oxygen in CO2 = 32/44 x 100 = 72.7%
Calculations of solutions: moles, concentration and volume
General Equation:
Concentration (mol / dm3) = Amount of substance (mol) ÷ Volume of solution (dm3)
This general equation is rearranged for the term as is asked in the question.
1. Calculating Moles
Equation:
Amount of Substance (mol) = Concentration x Volume of Solution (dm3)
Example:
Calculate the Moles of Solute Dissolved in 2 dm3 of a 0.1 mol / dm3 Solution
Concentration of Solution : 0.1 mol / dm3
Volume of Solution : 2 dm3
Moles of Solute = 0.1 x 2 = 0.2 mol (the dm3 above and below the line cancel out)
Amount of Solute = 0.2 mol
2. Calculating Concentration
Equation:
Concentration (mol / dm3) = Amount of substance (mol) ÷ Volume of solution (dm3)
Example:
25.0 cm3 of 0.050 mol / dm3 sodium carbonate was completely neutralised by 20.00 cm3 of dilute hydrochloric acid. Calculate the concentration in mol / dm3 of the hydrochloric acid.
Step 1 – Calculate the amount, in moles, of sodium carbonate reacted by rearranging the equation for amount of substance (mol) and dividing by 1000 to convert cm3 to dm3
Amount of Na2CO3 = (25.0 x 0.050) ÷ 1000 = 0.00125 mol
Step 2 – Calculate the amount, in moles, of hydrochloric acid reacted
1 mol of Na2CO3 reacts with 2 mol of HCl, so the Molar Ratio is 1 : 2
Therefore 0.00125 moles of Na2CO3 react with 0.00250 moles of HCl
Step 3 – Calculate the concentration, in mol / dm3 of the Hydrochloric Acid
1 dm3 = 1000 cm3
Volume of HCl = 20 ÷ 1000 = 0.0200 dm3
Concentration HCl (mol / dm3) = 0.00250 ÷ 0.0200 = 0.125
Concentration of Hydrochloric Acid = 0.125 mol / dm3
3. Calculating Volume
Equation:
Volume (dm3) = Amount of substance (mol) ÷ Concentration (mol / dm3)
Example:
Calculate the volume of hydrochloric acid of concentration 1.0 mol / dm3 that is required to react completely with 2.5g of calcium carbonate.
Step 1 – Calculate the amount, in moles, of calcium carbonate that reacts
Mr of CaCO3 is 100
Amount of CaCO3 = (2.5 ÷ 100) = 0.025 mol
Step 2 – Calculate the moles of hydrochloric acid required
CaCO3 + 2HCl → CaCl2 + H2O + CO2
1 mol of CaCO3 requires 2 mol of HCl
So 0.025 mol of CaCO3 Requires 0.05 mol of HCl
Step 3 – Calculate the volume of HCl Required
Volume = (Amount of Substance(mol) ÷ Concentration (mol / dm3)
= 0.05 ÷ 1.0
= 0.05 dm3 (the moles cancel out above and below the line)
Volume of Hydrochloric Acid = 0.05 dm3
The limiting reactant and reacting masses
Limiting reactant
- The limiting reactant is the reactant which is not present in excess in a reaction
- It is always the first reactant to be used up which then causes the reaction to stop
- In order to determine which reactant is the limiting reagent in a reaction, we have to consider the ratios of each reactant in the balanced equation
Example:
9.2g of sodium is reacted with 8.0g of sulfur to produce sodium sulfide, NaS. Which reactant is in excess and which is the limiting reactant?
Step 1 – Calculate the moles of each reactant
Moles = Mass ÷ Ar
Moles Na = 9.2/23 = 0.40
Moles S = 8.0/32 = 0.25
Step 2 – Write the balanced equation and determine the molar ratio
2Na + S → Na2S so the molar ratios is 2 : 1
Step 3 – Compare the moles. So to react completely 0.40 moles of Na require 0.20 moles of S and since there are 0.25 moles of S, then S is in excess. Na is therefore the limiting reactant.
Calculating reacting masses
- Chemical equations can be used to calculate the moles or masses of reactants and products
- Use information from the question to find the amount in moles of the substances being considered
- Identify the ratio between the substances using the balanced chemical equation
- Apply mole calculations to find answer
Example 1:
Calculate the Mass of Magnesium Oxide that can be made by completely burning 6 g of Magnesium in Oxygen
Magnesium (s) + Oxygen (g) → Magnesium Oxide (s)
Symbol Equation:
2Mg + O2 → 2MgO
Relative Formula Mass: Magnesium : 24 Magnesium Oxide : 40
Step 1 – Calculate the moles of Magnesium Used in reaction
Moles = Mass ÷ Mr Moles = 6 ÷ 24 = 0.25
Step 2 – Find the Ratio of Magnesium to Magnesium Oxide using the balanced Chemical Equation
Step 3 – Find the Mass of Magnesium Oxide
Moles of Magnesium Oxide = 0.25
Mass = Moles x Mr Mass = 0.25 x 40 = 10 g
Mass of Magnesium Oxide Produced = 10 g
Example 2:
Calculate the Mass, in Tonnes, of Aluminium that can be Produced from 51 Tonnes of Aluminium Oxide
Aluminium Oxide (s) → Aluminium (s) + Oxygen (g)
Symbol Equation:
2Al2O3 → 4Al + 3O2
Ar and Mr: Aluminium : 27 Oxygen : 16 Aluminium Oxide : 102
1 Tonne = 106 g
Step 1 – Calculate the moles of aluminium oxide used
Mass of Aluminium Oxide in Grams = 51 x 106 = 51,000,000 g
Moles = Mass ÷ Ar Moles = 51,000,000 ÷ 102 = 500,000
Step 2 – Find the ratio of aluminium oxide to aluminium using the balanced chemical equation
Step 3 – Find the mass of aluminium
Moles of aluminium = 1,000,000
Mass in grams = Moles x Ar Mass = 1,000,000 x 27 = 27,000,000
Mass in Tonnes = 27,000,000 ÷ 106 = 27 Tonnes
Mass of Aluminium Produced = 27 TonnesExtended Only
Using the Mole to Determine Empirical & Molecular Formulae
Empirical formula: gives the simplest whole number ratio of atoms of each element in the compound
- Calculated from knowledge of the ratio of masses of each element in the compound
Example:
A compound that contains 10 g of Hydrogen and 80 g of Oxygen has an Empirical Formula of H2O. This can be shown by the following calculations:
Amount of Hydrogen Atoms = Mass in grams ÷ Ar of Hydrogen = (10 ÷ 1) = 10 moles
Amount of Oxygen Atoms = Mass in grams ÷ Ar of Oxygen = (80 ÷ 16) = 5 moles
The ratio of moles of hydrogen atoms to moles of oxygen atoms:
Since equal numbers of moles of atoms contain the same number of atoms, the ratio of hydrogen atoms to oxygen atoms is 2:1
Hence the empirical formula is H2O
Molecular formula: gives the exact numbers of atoms of each element present in the formula of the compound
- Divide the relative formula mass of the molecular formula by the relative formula mass of the Empirical Formula
- Multiply the number of each element present in the Empirical Formula by this number to find the Molecular Formula
Relationship between Empirical and Molecular Formula:
Example:
The Empirical Formula of X is C4H10S1 and the Relative Formula Mass of X is 180. What is the Molecular Formula of X?
Relative Formula Mass: Carbon : 12 Hydrogen : 1 Sulfur : 32
Step 1 – Calculate Relative Formula Mass of Empirical Formula
(C x 4) + (H x 10) + (S x 1) = (12 x 4) + (1 x 10) + (32 x 1) = 90
Step 2 – Divide Relative Formula Mass of X by Relative Formula Mass of Empirical
Formula
180 / 90 = 2
Step 3 – Multiply Each Number of Elements by 2
(C4 x 2) + (H10 x 2) + (S1 x 2) = (C8) + (H20) + (S2)
Molecular Formula of X = C8H20S2Extended Only
Calculating Percentage Yield & Percentage Purity of the Product
Percentage yield
- This is the calculation of the percentage yield obtained from the theoretical yield
- In practice, you never get 100% yield in a chemical process for several reasons
- These include some reactants being left behind in the equipment, the reaction may be reversible or product may also be lost during separation stages
Equation:
Percentage Yield = (Yield Obtained / Theoretical Yield) x 100
Example:
In an experiment to displace copper from copper sulfate, 6.5 g of Zinc was added to an excess of copper (II) sulfate solution. The copper was filtered off, washed and dried. The mass of copper obtained was 4.8 g. Calculate the percentage yield of copper.
Equation Of Reaction:
Zn (s) + CuSO4 (aq)→ ZnSO4 (aq) + Cu (s)
Step 1: Calculate the Amount, in Moles of Zinc Reacted
Moles of Zinc = 6.5 ÷ 65 = 0.10 moles
Step 2: Calculate the Maximum Amount of Copper that could be formed from the
Molar ratio
Maximum Moles of Copper = 0.10 moles (Molar ratio is 1:1)
Step 3: Calculate the Maximum Mass of Copper that could be Formed
Maximum Mass of Copper = ( 0.10 x 64 ) = 6.4 g
Step 4: Calculate the Percentage of Yield of Copper
Percentage Yield = ( 4.8 ÷ 6.4 ) x 100 = 75%
Percentage Yield of Copper = 75%
Percentage purity
- Often the product you are trying to fabricate may become contaminated with unwanted substances such as unreacted reactants, catalysts etc.
Equation:
Percentage Purity = (Mass of pure substance / Mass of impure substance) x 100
Example:
In an experiment 7.0g of impure calcium carbonate were heated to a very high temperature and 2.5g of carbon dioxide were formed. Calculate the percentage purity of the calcium carbonate.
Equation Of Reaction:
CaCO3 (s) → CaO(s) + CO2 (g)
Step 1: Calculate the relative formula masses
1 mole CaCO3 → 1 mole CO2
40+12+(3×16) 12+(2×16)
100 → 44
Step 2: Calculate the theoretical mass of calcium carbonate used if pure
From 2.5g CO2 we would expect 2.5/44 x 100 = 5.68g
Step 3: Calculate the percentage purity
(Mass of pure substance / mass of impure substance) x 100
= 5.68/7.0 x 100
= 81.1%